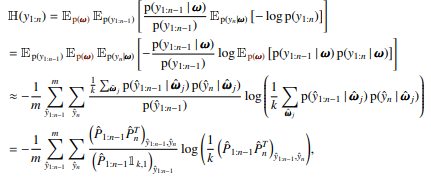This module helps compute joint entropies for dependent categorical variables given via a density $p((y_i)_i|w))$ in the Bayesian setting. We compute the density $p((y_i)_i)$ by marginalizing over $w$.
Two cases are implemented:
- exact joint entropies (which works for up 5 to joint variables depending on memory and # of classes);
- estimated joint entropies using importance sampling of configurations.
Note: "exact" based on the given draws of $w$. They are still an approximation because we do not integrate over $w$ but use Monte-Carlo samples.
Number of inference samples K:
K = 20
import torch
from toma import toma
from tqdm.auto import tqdm
To run tests, we need a few sampled distributions.
import numpy as np
def get_mixture_prob_dist(p1, p2, m):
return (1.0 - m) * np.asarray(p1) + m * np.asarray(p2)
p1 = [0.1, 0.2, 0.2, 0.5]
p2 = [0.5, 0.2, 0.1, 0.2]
y1_ws = [get_mixture_prob_dist(p1, p2, m) for m in np.linspace(0, 1, K)]
p1 = [0.1, 0.6, 0.2, 0.1]
p2 = [0.0, 0.5, 0.5, 0.0]
y2_ws = [get_mixture_prob_dist(p1, p2, m) for m in np.linspace(0, 1, K)]
def nested_to_tensor(*l):
return torch.stack(list(map(torch.as_tensor, l)))
ys_ws = nested_to_tensor(y1_ws, y2_ws, y1_ws, y2_ws, y1_ws, y2_ws, y1_ws, y2_ws)
Exact Joint Entropies
To compute exact joint entropies, we have to compute all possible configurations of the $y_i$ and evaluate $p(y_1, \dots, y_n)$ by averaging over $p(y_1, \dots, y_n|w)$.
The number of samples $M=C^N$, where $N$ is the number of variables in the joint and $C$ is the number of classes.
For this, we provide a class ExactJointEntropy that takes $K$ and starts with no variables in the joint.
In the Paper
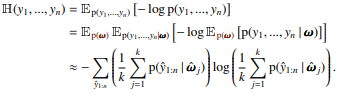
class ExactJointEntropy(JointEntropy):
joint_probs_M_K: torch.Tensor
def __init__(self, joint_probs_M_K: torch.Tensor):
self.joint_probs_M_K = joint_probs_M_K
@staticmethod
def empty(K: int, device=None, dtype=None) -> "ExactJointEntropy":
return ExactJointEntropy(torch.ones((1, K), device=device, dtype=dtype))
def compute(self) -> torch.Tensor:
probs_M = torch.mean(self.joint_probs_M_K, dim=1, keepdim=False)
nats_M = -torch.log(probs_M) * probs_M
entropy = torch.sum(nats_M)
return entropy
def add_variables(self, log_probs_N_K_C: torch.Tensor) -> "ExactJointEntropy":
assert self.joint_probs_M_K.shape[1] == log_probs_N_K_C.shape[1]
N, K, C = log_probs_N_K_C.shape
joint_probs_K_M_1 = self.joint_probs_M_K.t()[:, :, None]
probs_N_K_C = log_probs_N_K_C.exp()
# Using lots of memory.
for i in range(N):
probs_i__K_1_C = probs_N_K_C[i][:, None, :].to(joint_probs_K_M_1, non_blocking=True)
joint_probs_K_M_C = joint_probs_K_M_1 * probs_i__K_1_C
joint_probs_K_M_1 = joint_probs_K_M_C.reshape((K, -1, 1))
self.joint_probs_M_K = joint_probs_K_M_1.squeeze(2).t()
return self
def compute_batch(self, log_probs_B_K_C: torch.Tensor, output_entropies_B=None):
assert self.joint_probs_M_K.shape[1] == log_probs_B_K_C.shape[1]
B, K, C = log_probs_B_K_C.shape
M = self.joint_probs_M_K.shape[0]
if output_entropies_B is None:
output_entropies_B = torch.empty(B, dtype=log_probs_B_K_C.dtype, device=log_probs_B_K_C.device)
pbar = tqdm(total=B, desc="ExactJointEntropy.compute_batch", leave=False)
@toma.execute.chunked(log_probs_B_K_C, initial_step=1024, dimension=0)
def chunked_joint_entropy(chunked_log_probs_b_K_C: torch.Tensor, start: int, end: int):
chunked_probs_b_K_C = chunked_log_probs_b_K_C.exp()
b = chunked_probs_b_K_C.shape[0]
probs_b_M_C = torch.empty(
(b, M, C),
dtype=self.joint_probs_M_K.dtype,
device=self.joint_probs_M_K.device,
)
for i in range(b):
torch.matmul(
self.joint_probs_M_K,
chunked_probs_b_K_C[i].to(self.joint_probs_M_K, non_blocking=True),
out=probs_b_M_C[i],
)
probs_b_M_C /= K
output_entropies_B[start:end].copy_(
torch.sum(-torch.log(probs_b_M_C) * probs_b_M_C, dim=(1, 2)),
non_blocking=True,
)
pbar.update(end - start)
pbar.close()
return output_entropies_B
joint_entropy = ExactJointEntropy.empty(K, dtype=torch.double)
entropy = joint_entropy.add_variables(ys_ws[:4].log()).compute()
assert np.isclose(entropy, 4.6479, atol=0.1)
entropy
joint_entropy = ExactJointEntropy.empty(K, dtype=torch.float)
entropy = joint_entropy.add_variables(ys_ws[:4].log()).compute()
assert np.isclose(entropy, 4.6479, atol=0.1)
entropy
joint_entropy = ExactJointEntropy.empty(K, dtype=torch.float)
entropies = joint_entropy.add_variables(ys_ws[:4].log()).compute_batch(ys_ws.log())
assert np.allclose(entropies, [5.9735, 5.6362, 5.9735, 5.6362, 5.9735, 5.6362, 5.9735, 5.6362])
entropies
To compute approximate joint entropies, we have to sample possible configurations of the $y_i$ from $p(y_1, \dots, y_n|w)$ stratified by $p(w)$ and evaluate $p(y_1, \dots, y_n)$ by averaging over $p(y_1, \dots, y_n|w)$.
The number of samples is $M$, so we use $\frac{M}{K}$ samples per $w$.
For this, we provide a class SampledJointEntropy that takes $K$ and $M$, and implements the 'JointEntropy' interface.
To sample, we need a few helper functions.
def batch_multi_choices(probs_b_C, M: int):
"""
probs_b_C: Ni... x C
Returns:
choices: Ni... x M
"""
probs_B_C = probs_b_C.reshape((-1, probs_b_C.shape[-1]))
# samples: Ni... x draw_per_xx
choices = torch.multinomial(probs_B_C, num_samples=M, replacement=True)
choices_b_M = choices.reshape(list(probs_b_C.shape[:-1]) + [M])
return choices_b_M
def gather_expand(data, dim, index):
if gather_expand.DEBUG_CHECKS:
assert len(data.shape) == len(index.shape)
assert all(dr == ir or 1 in (dr, ir) for dr, ir in zip(data.shape, index.shape))
max_shape = [max(dr, ir) for dr, ir in zip(data.shape, index.shape)]
new_data_shape = list(max_shape)
new_data_shape[dim] = data.shape[dim]
new_index_shape = list(max_shape)
new_index_shape[dim] = index.shape[dim]
data = data.expand(new_data_shape)
index = index.expand(new_index_shape)
return torch.gather(data, dim, index)
gather_expand.DEBUG_CHECKS = False
class SampledJointEntropy(JointEntropy):
"""Random variables (all with the same # of categories $C$) can be added via `SampledJointEntropy.add_variables`.
`SampledJointEntropy.compute` computes the joint entropy.
`SampledJointEntropy.compute_batch` computes the joint entropy of the added variables with each of the variables in the provided batch probabilities in turn."""
sampled_joint_probs_M_K: torch.Tensor
def __init__(self, sampled_joint_probs_M_K: torch.Tensor):
self.sampled_joint_probs_M_K = sampled_joint_probs_M_K
@staticmethod
def empty(K: int, device=None, dtype=None) -> "SampledJointEntropy":
return SampledJointEntropy(torch.ones((1, K), device=device, dtype=dtype))
@staticmethod
def sample(probs_N_K_C: torch.Tensor, M: int) -> "SampledJointEntropy":
K = probs_N_K_C.shape[1]
# S: num of samples per w
S = M // K
choices_N_K_S = batch_multi_choices(probs_N_K_C, S).long()
expanded_choices_N_1_K_S = choices_N_K_S[:, None, :, :]
expanded_probs_N_K_1_C = probs_N_K_C[:, :, None, :]
probs_N_K_K_S = gather_expand(expanded_probs_N_K_1_C, dim=-1, index=expanded_choices_N_1_K_S)
# exp sum log seems necessary to avoid 0s?
probs_K_K_S = torch.exp(torch.sum(torch.log(probs_N_K_K_S), dim=0, keepdim=False))
samples_K_M = probs_K_K_S.reshape((K, -1))
samples_M_K = samples_K_M.t()
return SampledJointEntropy(samples_M_K)
def compute(self) -> torch.Tensor:
sampled_joint_probs_M = torch.mean(self.sampled_joint_probs_M_K, dim=1, keepdim=False)
nats_M = -torch.log(sampled_joint_probs_M)
entropy = torch.mean(nats_M)
return entropy
def add_variables(self, log_probs_N_K_C: torch.Tensor, M2: int) -> "SampledJointEntropy":
assert self.sampled_joint_probs_M_K.shape[1] == log_probs_N_K_C.shape[1]
sample_K_M1_1 = self.sampled_joint_probs_M_K.t()[:, :, None]
new_sample_M2_K = self.sample(log_probs_N_K_C.exp(), M2).sampled_joint_probs_M_K
new_sample_K_1_M2 = new_sample_M2_K.t()[:, None, :]
merged_sample_K_M1_M2 = sample_K_M1_1 * new_sample_K_1_M2
merged_sample_K_M = merged_sample_K_M1_M2.reshape((K, -1))
self.sampled_joint_probs_M_K = merged_sample_K_M.t()
return self
def compute_batch(self, log_probs_B_K_C: torch.Tensor, output_entropies_B=None):
assert self.sampled_joint_probs_M_K.shape[1] == log_probs_B_K_C.shape[1]
B, K, C = log_probs_B_K_C.shape
M = self.sampled_joint_probs_M_K.shape[0]
if output_entropies_B is None:
output_entropies_B = torch.empty(B, dtype=log_probs_B_K_C.dtype, device=log_probs_B_K_C.device)
pbar = tqdm(total=B, desc="SampledJointEntropy.compute_batch", leave=False)
@toma.execute.chunked(log_probs_B_K_C, initial_step=1024, dimension=0)
def chunked_joint_entropy(chunked_log_probs_b_K_C: torch.Tensor, start: int, end: int):
b = chunked_log_probs_b_K_C.shape[0]
probs_b_M_C = torch.empty(
(b, M, C),
dtype=self.sampled_joint_probs_M_K.dtype,
device=self.sampled_joint_probs_M_K.device,
)
for i in range(b):
torch.matmul(
self.sampled_joint_probs_M_K,
chunked_log_probs_b_K_C[i].to(self.sampled_joint_probs_M_K, non_blocking=True).exp(),
out=probs_b_M_C[i],
)
probs_b_M_C /= K
q_1_M_1 = self.sampled_joint_probs_M_K.mean(dim=1, keepdim=True)[None]
output_entropies_B[start:end].copy_(
torch.sum(-torch.log(probs_b_M_C) * probs_b_M_C / q_1_M_1, dim=(1, 2)) / M,
non_blocking=True,
)
pbar.update(end - start)
pbar.close()
return output_entropies_B
joint_entropy = SampledJointEntropy.empty(K, dtype=torch.double)
entropy = joint_entropy.add_variables(ys_ws[:4].log(), 100000).compute()
print(entropy)
assert np.isclose(entropy, 4.6479, atol=0.1)
joint_entropy = SampledJointEntropy.empty(K, dtype=torch.double)
entropy = joint_entropy.add_variables(ys_ws[:4].log(), 100000).compute()
print(entropy)
assert np.isclose(entropy, 4.6479, atol=0.1)
joint_entropy = SampledJointEntropy.empty(K, dtype=torch.float)
entropies = joint_entropy.add_variables(ys_ws[:4].log(), 10000).compute_batch(ys_ws.log())
print(entropies)
assert np.allclose(
entropies,
[5.9735, 5.6362, 5.9735, 5.6362, 5.9735, 5.6362, 5.9735, 5.6362],
atol=0.05,
)
class DynamicJointEntropy(JointEntropy):
inner: JointEntropy
log_probs_max_N_K_C: torch.Tensor
N: int
M: int
def __init__(self, M: int, max_N: int, K: int, C: int, dtype=None, device=None):
self.M = M
self.N = 0
self.max_N = max_N
self.inner = ExactJointEntropy.empty(K, dtype=dtype, device=device)
self.log_probs_max_N_K_C = torch.empty((max_N, K, C), dtype=dtype, device=device)
def add_variables(self, log_probs_N_K_C: torch.Tensor) -> "DynamicJointEntropy":
C = self.log_probs_max_N_K_C.shape[2]
add_N = log_probs_N_K_C.shape[0]
assert self.log_probs_max_N_K_C.shape[0] >= self.N + add_N
assert self.log_probs_max_N_K_C.shape[2] == C
self.log_probs_max_N_K_C[self.N : self.N + add_N] = log_probs_N_K_C
self.N += add_N
num_exact_samples = C ** self.N
if num_exact_samples > self.M:
self.inner = SampledJointEntropy.sample(self.log_probs_max_N_K_C[: self.N].exp(), self.M)
else:
self.inner.add_variables(log_probs_N_K_C)
return self
def compute(self) -> torch.Tensor:
return self.inner.compute()
def compute_batch(self, log_probs_B_K_C: torch.Tensor, output_entropies_B=None) -> torch.Tensor:
"""Computes the joint entropy of the added variables together with the batch (one by one)."""
return self.inner.compute_batch(log_probs_B_K_C, output_entropies_B)
joint_entropy = DynamicJointEntropy(256, 8, K, 4, dtype=torch.double)
entropy = joint_entropy.add_variables(ys_ws[:4].log()).compute()
print(entropy)
assert np.isclose(entropy, 4.6479, atol=0.1)
assert type(joint_entropy.inner) == ExactJointEntropy
entropy = joint_entropy.add_variables(ys_ws[4:].log()).compute()
print(entropy)
assert np.isclose(entropy, 9.2756, atol=0.5)
assert type(joint_entropy.inner) == SampledJointEntropy